역전파 (Back Propagation)
14 Mar 2020 | Deep-Learning
Back Propagation
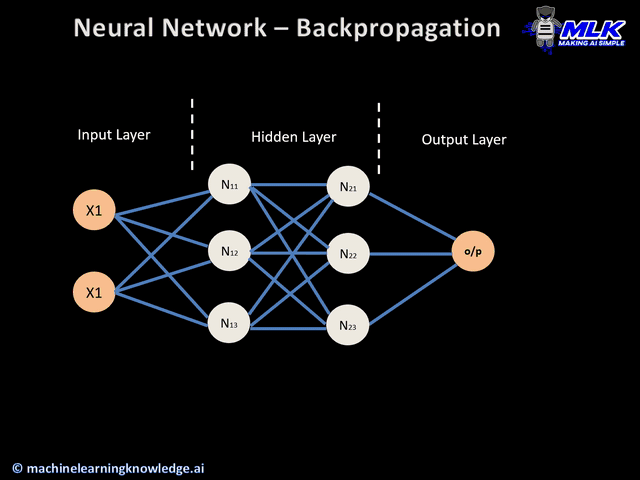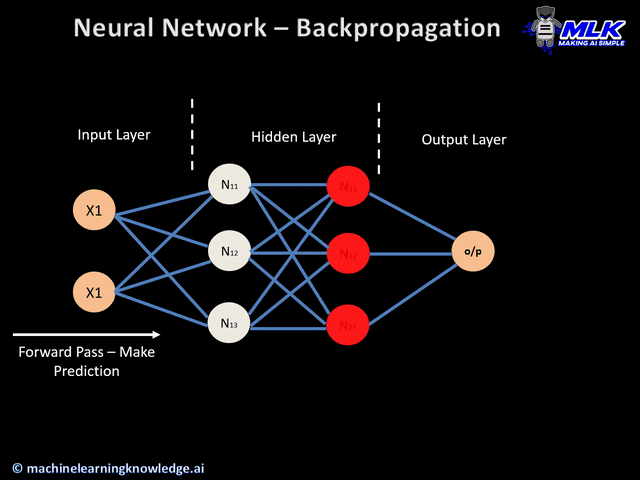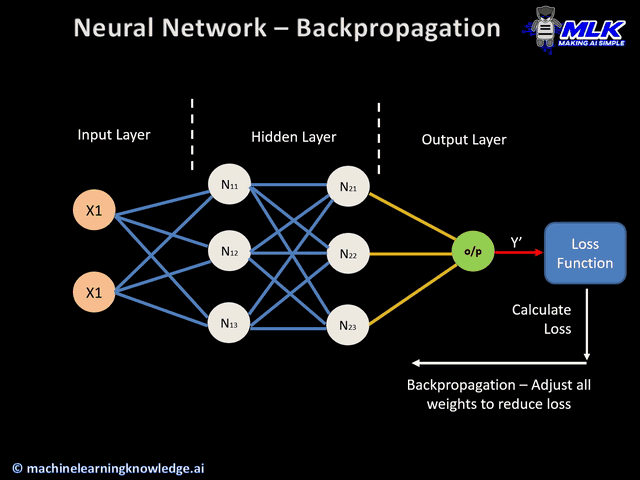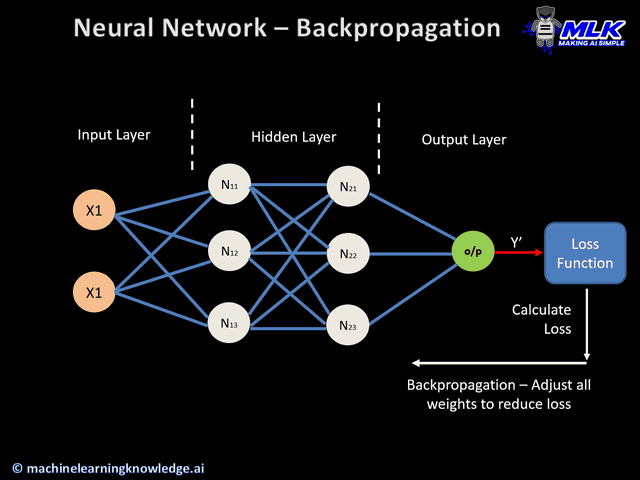
이번 게시물에서는 신경망 정보 전달의 핵심인 순전파와 역전파에 대해서 알아보겠습니다. 이 두 가지가 잘 일어나야 정보가 제대로 전달되어 손실을 줄이는 방향으로 학습이 잘 일어날 수 있겠지요. 아래는 신경망의 대략적인 흐름을 나타낸 이미지입니다.
이미지 출처 : machinelearningknowledge.ai
Forward Propagation
순전파(Forward Propagation)은 (입력층 → 출력층)의 방향으로 계산하는 과정입니다. 신호와 가중치를 곱한 값 출력층까지 차례대로 계산합니다. 아래 이미지를 보면서 순전파의 계산이 어떻게 진행되는지를 알아보겠습니다. 입력층의 노드가 2개이고 은닉층의 노드가 3개, 출력층의 노드가 1개인 신경망이 있다고 해보겠습니다. 이 인스턴스의 신호 $x_1, x_2$ 의 값은 1이며 레이블 $y$ 는 0입니다.

이미지 출처 : packtpub.com/book/big_data_and_business_intelligence
모든 층에 활성화 함수로 시그모이드(로지스틱) 함수를 사용한다면 은닉층의 히든노드에 들어갈 값 $\text{Sigmoid}(h)$는 아래의 수식을 통해서 구할 수 있습니다. $h_1,h_2,h_3$ 은 위쪽 노드부터 활성화 함수에 들어가는 값을 나타냅니다.
\[h_1 = 1 \times 0.8 + 1 \times 0.2 = 1.0, \quad \text{Sigmoid}(h_1) = 0.73 \\
h_2 = 1 \times 0.4 + 1 \times 0.9 = 1.3, \quad \text{Sigmoid}(h_2) = 0.79 \\
h_3 = 1 \times 0.3 + 1 \times 0.5 = 0.8, \quad \text{Sigmoid}(h_3) = 0.69\]
이제 은닉층에 들어갈 값을 모두 구했으니 출력되는 값 $\hat{y}$ 를 구해보겠습니다.
\[\hat{y} = 0.73 \times 0.3 + 0.79 \times 0.5 + 0.69 \times 0.9 = 1.235\]
이렇게 출력값을 구해내기 까지의 과정을 순전파라고 합니다.
Back Propagation
위 순전파 과정에서 실제의 레이블 $y=0$ 이지만 예측 레이블은 $\hat{y} = 1.235$ 입니다. $1.235$ 의 오차가 발생했네요. 이제 손실 함수(Loss function)을 통해 계산한 손실을 줄이는 방향으로 학습할 차례입니다. 각 노드에 손실 정보를 전달하는 과정을 역전파(Back propagation)라고 합니다. 손실 정보는 (출력층 → 입력층)의 방향으로 전달되기 때문에 ‘역’전파라는 이름이 붙었습니다.
먼저 연쇄 법칙(Chain rule)에 대해 알아보겠습니다. 미분값을 전달하는 역전파를 이해하기 위해서는 필수적으로 알아야 하는 개념이지요. 연쇄 법칙은 합성 함수의 도함수를 각 함수의 도함수의 곱으로 나타내는 방식입니다. 간단한 예를 들어보겠습니다. 함수 $z = (x+y)^2$ 가 있다고 해보겠습니다. 이 함수를 전개한 뒤에 $x$ 로 편미분하면 아래와 같은 편도함수를 구할 수 있습니다.
\[\frac{\partial z}{\partial x} = \frac{\partial (x^2 + 2xy+y^2)}{\partial x} = 2x + 2y\]
이를 $t = x+y$ 를 사용하여 아래와 같이 치환한 뒤에 연쇄 법칙을 사용하여 편도함수를 구해보겠습니다.
\[z = t^2, \quad t=x+y\]
연쇄 법칙을 사용하면 $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}$ 로 나타낼 수 있으므로 아래와 같이 편도함수를 구할 수 있습니다.
\[\begin{aligned}
\frac{\partial z}{\partial x} &= \frac{\partial z}{\partial t} \frac{\partial t}{\partial x} \\
&= 2t \cdot 1 = 2t
\end{aligned}\]
이제 본격적으로 역전파에 대해 알아보지요. 순전파에서 신경망이 수행하는 연산을 단순화하여 가중치 $x,y$ 로부터 출력 $z$를 내어 놓는 임의의 함수 $z = f(x,y)$ 라고 해보겠습니다. 원래의 손실 함수를 $L$이라고 하면 이를 개선하기 위한 미분은 $\frac{\partial L}{\partial z}$ 가 됩니다.
이를 각 가중치 $x, y$ 에 대하여 편미분한 값으로 나누어 가지게 됩니다. 아래는 이 과정을 잘 보여주는 그림입니다.
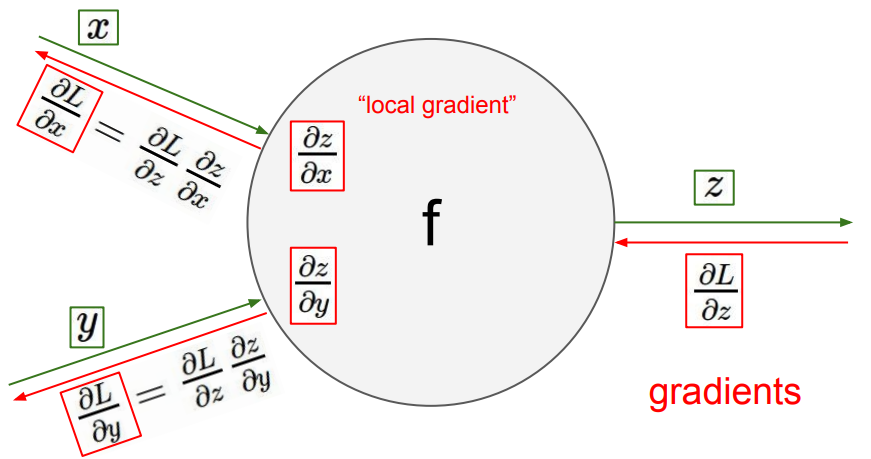
이미지 출처 : bishwarup307.github.io
역전파는 이 과정을 신경망의 모든 노드에 대해서 실행합니다. 예시를 통해 역전파가 일어나는 과정을 알아보겠습니다. 아래는 이진분류 문제에 대해서 100번의 반복 학습 동안의 노드의 가중치, 손실값, 결정 경계가 변하는 모습을 보여주는 이미지입니다.
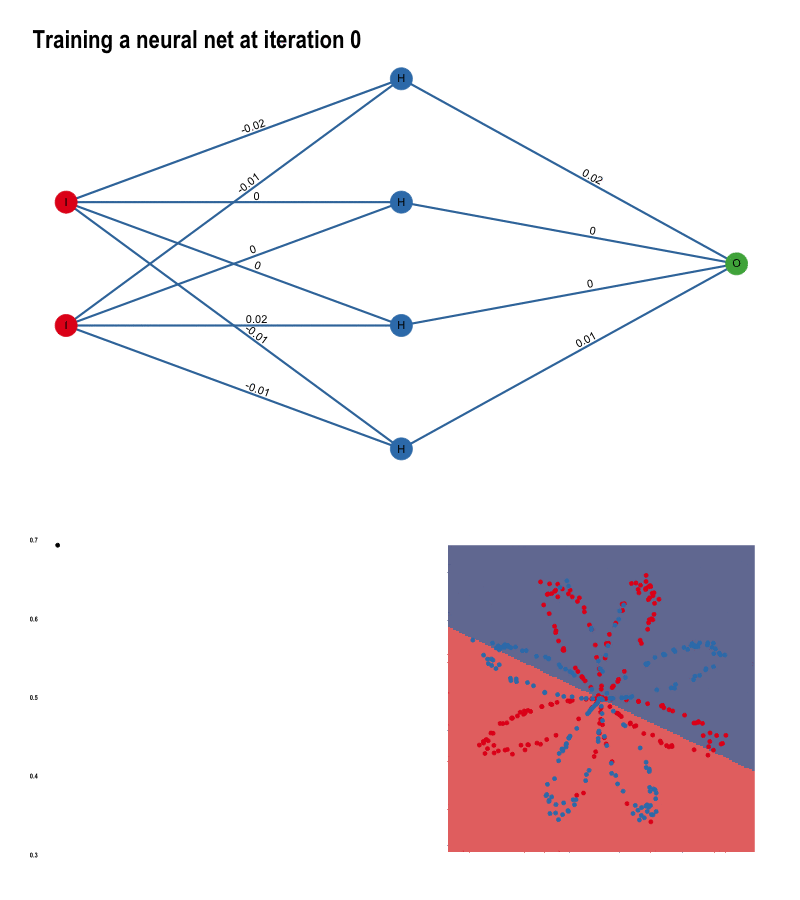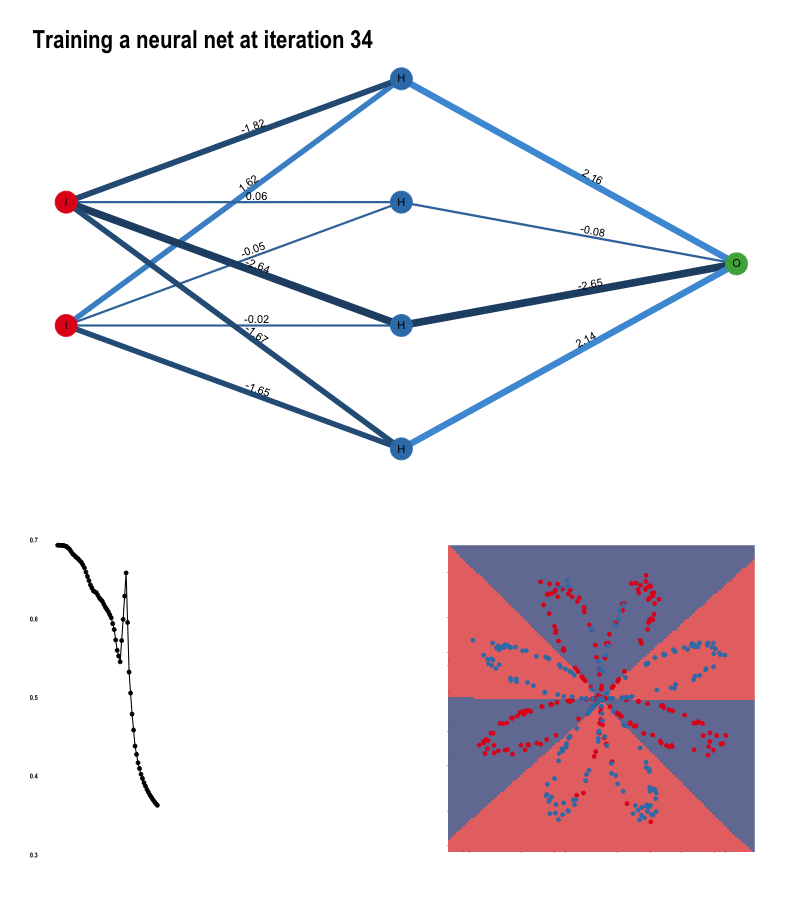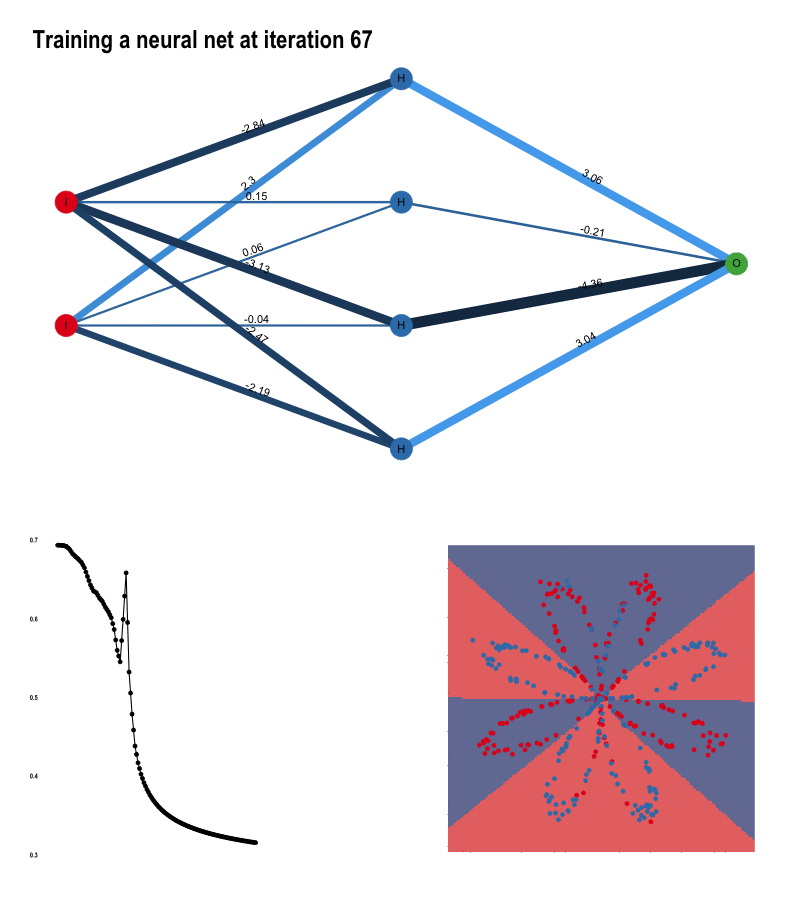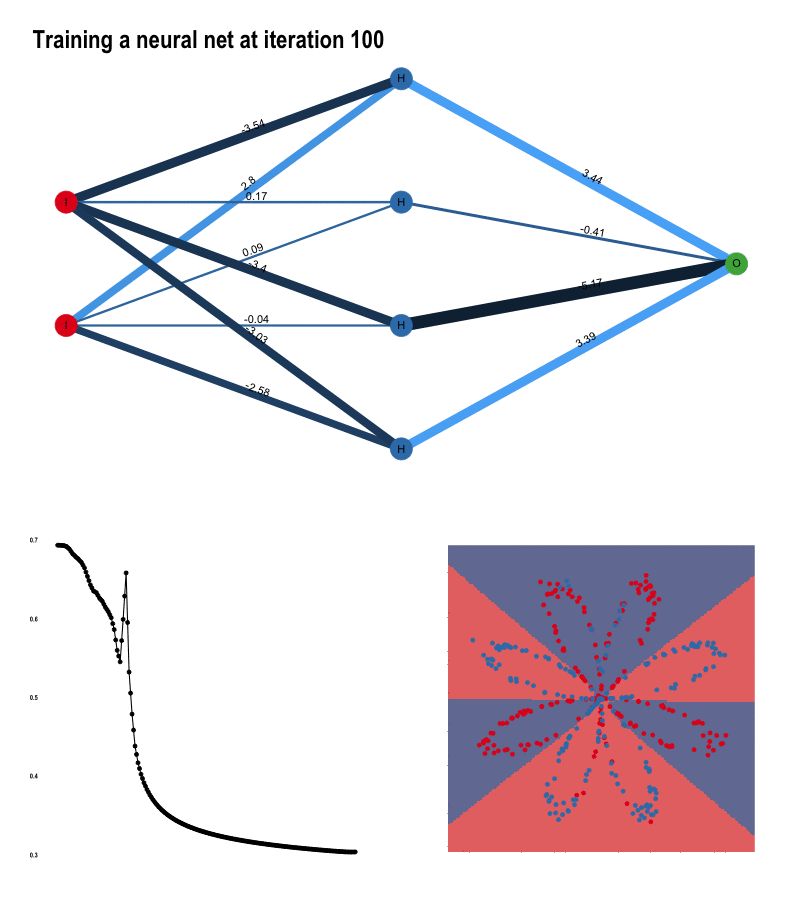
이미지 출처 : tamaszilagyi.com
다음으로 가중치가 어디서부터 어떻게 개선되는 지를 결정하는 가중치 초기화(Weight initialization)와 옵티마이저(Optimizer)에 대해서 알아보도록 하겠습니다.
Back Propagation
이번 게시물에서는 신경망 정보 전달의 핵심인 순전파와 역전파에 대해서 알아보겠습니다. 이 두 가지가 잘 일어나야 정보가 제대로 전달되어 손실을 줄이는 방향으로 학습이 잘 일어날 수 있겠지요. 아래는 신경망의 대략적인 흐름을 나타낸 이미지입니다.

이미지 출처 : machinelearningknowledge.ai
Forward Propagation
순전파(Forward Propagation)은 (입력층 → 출력층)의 방향으로 계산하는 과정입니다. 신호와 가중치를 곱한 값 출력층까지 차례대로 계산합니다. 아래 이미지를 보면서 순전파의 계산이 어떻게 진행되는지를 알아보겠습니다. 입력층의 노드가 2개이고 은닉층의 노드가 3개, 출력층의 노드가 1개인 신경망이 있다고 해보겠습니다. 이 인스턴스의 신호 $x_1, x_2$ 의 값은 1이며 레이블 $y$ 는 0입니다.

이미지 출처 : packtpub.com/book/big_data_and_business_intelligence
모든 층에 활성화 함수로 시그모이드(로지스틱) 함수를 사용한다면 은닉층의 히든노드에 들어갈 값 $\text{Sigmoid}(h)$는 아래의 수식을 통해서 구할 수 있습니다. $h_1,h_2,h_3$ 은 위쪽 노드부터 활성화 함수에 들어가는 값을 나타냅니다.
\[h_1 = 1 \times 0.8 + 1 \times 0.2 = 1.0, \quad \text{Sigmoid}(h_1) = 0.73 \\ h_2 = 1 \times 0.4 + 1 \times 0.9 = 1.3, \quad \text{Sigmoid}(h_2) = 0.79 \\ h_3 = 1 \times 0.3 + 1 \times 0.5 = 0.8, \quad \text{Sigmoid}(h_3) = 0.69\]이제 은닉층에 들어갈 값을 모두 구했으니 출력되는 값 $\hat{y}$ 를 구해보겠습니다.
\[\hat{y} = 0.73 \times 0.3 + 0.79 \times 0.5 + 0.69 \times 0.9 = 1.235\]이렇게 출력값을 구해내기 까지의 과정을 순전파라고 합니다.
Back Propagation
위 순전파 과정에서 실제의 레이블 $y=0$ 이지만 예측 레이블은 $\hat{y} = 1.235$ 입니다. $1.235$ 의 오차가 발생했네요. 이제 손실 함수(Loss function)을 통해 계산한 손실을 줄이는 방향으로 학습할 차례입니다. 각 노드에 손실 정보를 전달하는 과정을 역전파(Back propagation)라고 합니다. 손실 정보는 (출력층 → 입력층)의 방향으로 전달되기 때문에 ‘역’전파라는 이름이 붙었습니다.
먼저 연쇄 법칙(Chain rule)에 대해 알아보겠습니다. 미분값을 전달하는 역전파를 이해하기 위해서는 필수적으로 알아야 하는 개념이지요. 연쇄 법칙은 합성 함수의 도함수를 각 함수의 도함수의 곱으로 나타내는 방식입니다. 간단한 예를 들어보겠습니다. 함수 $z = (x+y)^2$ 가 있다고 해보겠습니다. 이 함수를 전개한 뒤에 $x$ 로 편미분하면 아래와 같은 편도함수를 구할 수 있습니다.
\[\frac{\partial z}{\partial x} = \frac{\partial (x^2 + 2xy+y^2)}{\partial x} = 2x + 2y\]이를 $t = x+y$ 를 사용하여 아래와 같이 치환한 뒤에 연쇄 법칙을 사용하여 편도함수를 구해보겠습니다.
\[z = t^2, \quad t=x+y\]연쇄 법칙을 사용하면 $\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}$ 로 나타낼 수 있으므로 아래와 같이 편도함수를 구할 수 있습니다.
\[\begin{aligned} \frac{\partial z}{\partial x} &= \frac{\partial z}{\partial t} \frac{\partial t}{\partial x} \\ &= 2t \cdot 1 = 2t \end{aligned}\]이제 본격적으로 역전파에 대해 알아보지요. 순전파에서 신경망이 수행하는 연산을 단순화하여 가중치 $x,y$ 로부터 출력 $z$를 내어 놓는 임의의 함수 $z = f(x,y)$ 라고 해보겠습니다. 원래의 손실 함수를 $L$이라고 하면 이를 개선하기 위한 미분은 $\frac{\partial L}{\partial z}$ 가 됩니다.
이를 각 가중치 $x, y$ 에 대하여 편미분한 값으로 나누어 가지게 됩니다. 아래는 이 과정을 잘 보여주는 그림입니다.

이미지 출처 : bishwarup307.github.io
역전파는 이 과정을 신경망의 모든 노드에 대해서 실행합니다. 예시를 통해 역전파가 일어나는 과정을 알아보겠습니다. 아래는 이진분류 문제에 대해서 100번의 반복 학습 동안의 노드의 가중치, 손실값, 결정 경계가 변하는 모습을 보여주는 이미지입니다.

이미지 출처 : tamaszilagyi.com
다음으로 가중치가 어디서부터 어떻게 개선되는 지를 결정하는 가중치 초기화(Weight initialization)와 옵티마이저(Optimizer)에 대해서 알아보도록 하겠습니다.

Comments